深度学习中常见评价指标 Acc、Recall、F1、RC、Roc、AUC、IOU、AP、mAP 2022-04-12
总共内容包含 Acc、Recall、F1、RC、Roc、AUC、IOU、AP、mAP
所有复杂问题都是简单问题的重复， 为了理解所有指标，首先需了解“四大天王”与“三大护法”
四大天王——TP|FP TN|FN
我们认为positive代表了阳性（或者说正样本）， 而Negative代表了阴性（负样本)，那么在二分类中我们根据猜测的对错很容易排列出2x2种情况：
| True | False | |
|---|---|---|
| Positive | TP(猜对了阳) | FP(猜错了阳) |
| Negative | TN(猜对了阴) | FN(猜错了阴) |
其中左半边表示真值和我的猜测一致（猜对了），右半边表示真值和我的猜测不一致（猜错了）；
上半边表示猜测阳性的全体 $P$，下半边表示猜测阴性的全体$N$。
TP+FN表示真值阳性的全体，TN+FP表示真值阴性的全体。
三大护法——Pre、ACC、Recall
根据四大金刚，我们容易得出常见模型中的三个评价指标， (为什么不能只看一个呢？因为容易被“浮云遮望眼”)
Pre(Precision 精确率又称查准率)
精确和准确在中文上看起来是一个意思，但实际上有微小的区别；
我们可以通过投标的例子来理解什么是精确，什么是准确。
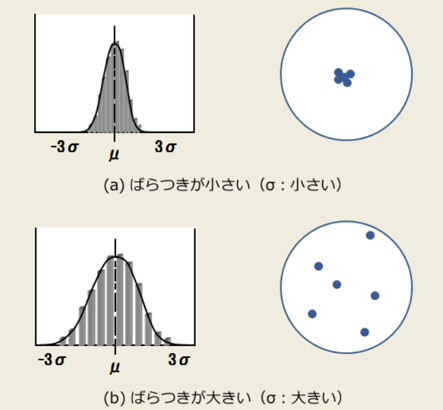从上图可知，精确率高的数据其标准差较小，也就是“我投中了，投中的差别不大”;在二分类中或者说判断是否阳性中，我们关注的重点是在我对阳性的判断中，是否判断对了(存不存在错判阳性的偏差）；如果精确率高，就说明我预测阳性偏差小，阳性就是真的阳性，较少出差错。
总结来说，精确率高指的是“我对正例判断出差错（偏差）的情况怎么样？”，也就是：
$$
Precision = \frac{TP}{P} = \frac{TP}{TP+FP}
$$
精确率越高，说明我对正例/阳性判断的偏差越小，也就是TP占总判断阳性中的比例越大。
这时候可能会有聪明的同学问了，那为什么我们不考虑对负例判断的偏差呢，比如构建一个TN/TN+FN的指标？
其实是有的，一般的，Pre还有更深入的名字叫“positive predictive value (PPV)”，显然也有对应的“Negative predictive value (NPV) ” 只是因为负样本通常较少，正样本较多；所以把PPV作为一个更常用的指标，归为精确率。
计算精确率的代码示例（使用PyTorch）：
import torch
def precision(preds, labels):
TP = torch.sum((preds == 1) & (labels == 1)).item()
FP = torch.sum((preds == 1) & (labels == 0)).item()
precision = TP / (TP + FP) if (TP + FP) > 0 else 0
return precision
# 示例
preds = torch.tensor([1, 0, 1, 1, 0])
labels = torch.tensor([1, 0, 0, 1, 0])
print("Precision:", precision(preds, labels))
ACC(Accuracy 准确率)
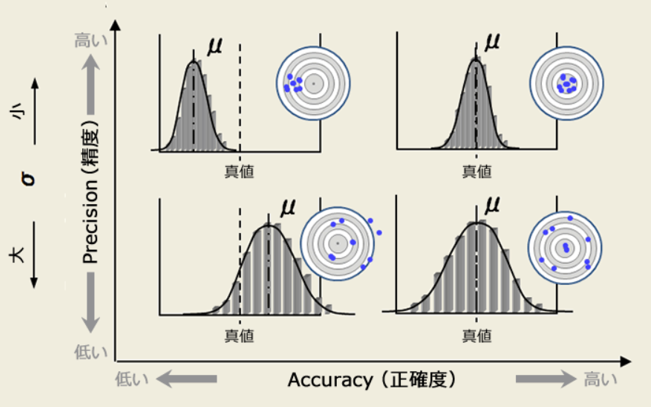
为什么说精准但“精确不一定准确呢”？
你可以这么想，精密仪器显然是为了误差小，那精密仪器一定能得到准确结果吗？————答案是不一定，比如你没有调零!(做过大物实验的朋友都知道~)
没有调零就好像y=kx+b中多了一个b，也就是投标图像中的“整体偏移真值” （下图的上半部分）
虽然很精确，但很不准确！！
准确率更容易理解，准确率考 虑的是更“全局”的结果是否正确，
也就是在我所有预测的结果中，我到底预测的“好不好”，
即：
$$
Accuracy = \frac{TP+TN}{所有预测} = \frac{TP+TN}{TP+FP+TN+FN}
$$
计算准确率的代码示例（使用PyTorch）：
import torch
def accuracy(preds, labels):
correct = torch.sum(preds == labels).item()
total = labels.size(0)
accuracy = correct / total
return accuracy
# 示例
preds = torch.tensor([1, 0, 1, 1, 0])
labels = torch.tensor([1, 0, 0, 1, 0])
print("Accuracy:", accuracy(preds, labels))
Recall(召回率又称查全率)
顾名思义，查全的意思就是“我查的全不全”，我是否把所有的阳性覆盖到了（阳性全体为P），
$$
Recall = \frac{TP}{阳性全体}= \frac{TP}{TP+FN}
$$
有时候查全率很高，但精确率很低。
比如我有3个阳性，97个阴性。我预测100个全为阳性（此时P=100且TP=3，FP=97），0个阴性；此时查全率为：3/3=100% ！
但此时精确率为：3%。。。。。这显然是没有意义的。
有时候精确率很高，但查全率很低。
比如我还是有3个阳性，97个阴性。我刚好预测对某1个为阳性（此时P=1且TP=1，FP=0），99个阴性；此时精确率为：100% ！
但此时查全率为：33.333%。。。。。这显然也是意义不大的。
查全率与精确率存在互逆关系
我们能够隐约发现查全率和精确率的互逆关系，但究竟是为什么呢？
仔细观察可以发现，Recall和Pre只在分母有差别，其中Recall的分母是TP+FN【不变量】，而Pre的分母是TP+FP【可变量】。
为了提高Recall，我们需要增大TP，而分母不变；
但Pre中如果TP增加了FP也会跟着增加（我需要判断的东西变多了，精确率会下降，错误的概率会变大），分子的TP增加小于分母的TP+FP总体的增加。所以查全率和精确率是互逆的。
计算召回率的代码示例（使用PyTorch）：
import torch
def recall(preds, labels):
TP = torch.sum((preds == 1) & (labels == 1)).item()
FN = torch.sum((preds == 0) & (labels == 1)).item()
recall = TP / (TP + FN) if (TP + FN) > 0 else 0
return recall
# 示例
preds = torch.tensor([1, 0, 1, 1, 0])
labels = torch.tensor([1, 0, 0, 1, 0])
print("Recall:", recall(preds, labels))
F1、RPC、Roc、AUC
在充分了解了四大金刚与三大护法后，我们进一步来研究他们的衍生变体：
F1-score
F1-score 是精确率（Precision）和召回率（Recall）的调和平均数，用于综合衡量模型的精确性和完整性。其计算公式为：
$$ F1 = 2 \times \frac{Precision \times Recall}{Precision + Recall} $$
F1-score 在精确率和召回率之间取得了平衡，尤其适用于类别不平衡的情况。当需要同时考虑精确率和召回率时，F1-score 是一个很好的指标。
优势：
- 综合考虑了精确率和召回率，避免了只关注其中一个指标带来的偏差。
- 在类别不平衡的情况下，能够更客观地反映模型性能。
劣势：
- 无法区分假阳性和假阴性对模型的不同影响。
- 当需要更细粒度地评估模型时，F1-score 可能不够全面。
计算F1-score的代码示例（使用PyTorch）：
import torch
def f1_score(preds, labels):
TP = torch.sum((preds == 1) & (labels == 1)).item()
FP = torch.sum((preds == 1) & (labels == 0)).item()
FN = torch.sum((preds == 0) & (labels == 1)).item()
precision = TP / (TP + FP) if (TP + FP) > 0 else 0
recall = TP / (TP + FN) if (TP + FN) > 0 else 0
if (precision + recall) == 0:
return 0
f1 = 2 * (precision * recall) / (precision + recall)
return f1
# 示例
preds = torch.tensor([1, 0, 1, 1, 0])
labels = torch.tensor([1, 0, 0, 1, 0])
print("F1 Score:", f1_score(preds, labels))
RPC (Precision-Recall Curve) 查准率-召回率曲线
RPC 是通过绘制精确率（Precision）与召回率（Recall）之间的关系曲线，来可视化模型在不同阈值下的性能表现。曲线下的面积（一般称为 AUC-PR）也是评估模型性能���重要指标。
绘制方法：
- 选择一组不同的阈值。
- 对每个阈值，计算对应的精确率和召回率。
- 将这些点连接起来，形成精确率-召回率曲线。
应用场景：
- 特别适用于类别不平衡的问题，如信息检索、推荐系统等。
- 当关心模型对少数类的表现时，RPC 提供了更直观的评估方式。
特点：
- 曲线越接近右上角，模型性能越好。
- 能够展示模型在不同权衡下的表现，帮助选择最合适的阈值。
计算RPC的代码示例（使用sklearn库）：
import torch
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve, auc
def plot_pr_curve(labels, scores):
preds = scores.detach().cpu().numpy()
true = labels.detach().cpu().numpy()
precision, recall, thresholds = precision_recall_curve(true, preds)
auc_pr = auc(recall, precision)
plt.figure()
plt.plot(recall, precision, label=f'AUC-PR = {auc_pr:.2f}')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision-Recall Curve')
plt.legend()
plt.show()
# 示例
labels = torch.tensor([1, 0, 1, 1, 0])
scores = torch.tensor([0.9, 0.2, 0.8, 0.7, 0.1])
plot_pr_curve(labels, scores)
ROC (Receiver Operating Characteristic) 曲线
ROC曲线是一种评估二分类模型性能的工具，通过绘制真正率（TPR）与假正率（FPR）的关系，来展示模型在不同阈值下的表现。
定义：
- 真正率 (TPR) / 召回率 (Recall)： $\frac{TP}{TP + FN}$
- 假正率 (FPR)： $\frac{FP}{FP + TN}$
绘 制方法：
- 选择一组不同的阈值。
- 对每个阈值，计算对应的 TPR 和 FPR。
- 将这些点连接起来，形成 ROC 曲线。
特点：
- 曲线越接近左上角，模型性能越好。
- 曲线下的面积（AUC-ROC）越大，模型性能越优。
应用场景：
- 广泛应用于医学诊断、信用评分等领域。
- 适用于类别分布平衡或不平衡的情况。
计算ROC的代码示例（使用sklearn库）：
import torch
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, auc
def plot_roc_curve(labels, scores):
preds = scores.detach().cpu().numpy()
true = labels.detach().cpu().numpy()
fpr, tpr, thresholds = roc_curve(true, preds)
roc_auc = auc(fpr, tpr)
plt.figure()
plt.plot(fpr, tpr, label=f'AUC-ROC = {roc_auc:.2f}')
plt.plot([0, 1], [0, 1], 'k--') # 随机分类器的性能
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend()
plt.show()
# 示例
labels = torch.tensor([1, 0, 1, 1, 0])
scores = torch.tensor([0.9, 0.2, 0.8, 0.7, 0.1])
plot_roc_curve(labels, scores)
AUC (Area Under the Curve)
AUC 是 ROC 曲线下的面积，用于量化模型的整体性能。其取值范围为 [0.5, 1]，其中 0.5 表示模型没有预测能力，相当于随机猜测；1 表示模型具有完美的预测能力。
计算方法：
- 通过数值积分方法计算 ROC 曲线下的面积。
- 常用的方法包括梯形法则等。
意义：
- AUC 越接近 1，表示模型的区分能力越强。
- 当比较多个模型时，AUC 是一个比较直观且有效的指标。
优势：
- 对类别不平衡不敏感，能够全面评估模型。
- 独立于预测阈值，提供了模型的整体性能评估。
劣势：
- 对于某些具体应用场景，AUC 可能无法反映模型的实际需求。
- 需要了解模型的概率输出，才能正确计算 AUC。
计算AUC的代码示例（使用sklearn库）：
import torch
from sklearn.metrics import roc_auc_score
def calculate_auc(labels, scores):
preds = scores.detach().cpu().numpy()
true = labels.detach().cpu().numpy()
auc_score = roc_auc_score(true, preds)
return auc_score
# 示例
labels = torch.tensor([1, 0, 1, 1, 0])
scores = torch.tensor([0.9, 0.2, 0.8, 0.7, 0.1])
print("AUC-ROC:", calculate_auc(labels, scores))
IOU、AP、mAP
除了上述常见的评价指标，机器学习和深度学习中还常用以下指标来评估模型，特别是在目标检测任务中：
IOU (Intersection Over Union)
IOU 是用于衡量预测框与真实框重叠程度的指标，其计算公式为：
$$ IOU = \frac{预测框 \cap 真实框}{预测框 \cup 真实框} $$
意义：
- IOU 值越大，表示预测框与真实框的重叠程度越高，预测越准确。
- 常用于目标检测任务中，作为判断预测结果是否为真正例的标准。
应用场景：
- 目标检测、实例分割等任务中，用于评估边界框的准确性。
计算IOU的代码示例（使用numpy）：
import numpy as np
def iou(box1, box2):
# box = [x1, y1, x2, y2]
x1 = max(box1[0], box2[0])
y1 = max(box1[1], box2[1])
x2 = min(box1[2], box2[2])
y2 = min(box1[3], box2[3])
inter_area = max(0, x2 - x1) * max(0, y2 - y1)
area1 = (box1[2] - box1[0]) * (box1[3] - box1[1])
area2 = (box2[2] - box2[0]) * (box2[3] - box2[1])
union_area = area1 + area2 - inter_area
return inter_area / union_area if union_area > 0 else 0
# 示例
box_pred = [50, 50, 150, 150]
box_true = [100, 100, 200, 200]
print("IOU:", iou(box_pred, box_true))
AP (Average Precision)
AP 是在单个类别上的平均精度，通常 通过计算 P-R 曲线下的面积来获得。
计算方法：
- 对每个预测结果按照置信度进行排序。
- 逐步增加阈值，计算对应的精确率和召回率。
- 通过插值方法计算 P-R 曲线下的面积，即为 AP 值。
意义：
- AP 值越高，表示模型在该类别上的检测性能越好。
计算AP的代码示例（使用sklearn库）：
import torch
from sklearn.metrics import average_precision_score
def calculate_ap(pred_boxes, pred_scores, gt_boxes, iou_threshold=0.5):
"""计算单个类别的AP值
Args:
pred_boxes: 预测框列表 shape=(N,4) [x1,y1,x2,y2]
pred_scores: 预测分数列表 shape=(N,)
gt_boxes: 真实框列表 shape=(M,4)
iou_threshold: IOU阈值
"""
# 按置信度降序排序
order = np.argsort(-pred_scores)
pred_boxes = pred_boxes[order]
pred_scores = pred_scores[order]
# 计算每个预测框与真实框的IOU
ious = np.zeros((len(pred_boxes), len(gt_boxes)))
for i, pred in enumerate(pred_boxes):
for j, gt in enumerate(gt_boxes):
ious[i,j] = calculate_iou(pred, gt)
# 计算precision和recall
tp = np.zeros(len(pred_boxes))
fp = np.zeros(len(pred_boxes))
gt_matched = np.zeros(len(gt_boxes))
for i in range(len(pred_boxes)):
# 找到最大IOU的真实框
max_iou_idx = np.argmax(ious[i])
max_iou = ious[i][max_iou_idx]
if max_iou >= iou_threshold and not gt_matched[max_iou_idx]:
tp[i] = 1
gt_matched[max_iou_idx] = 1
else:
fp[i] = 1
# 累积求和
tp_cumsum = np.cumsum(tp)
fp_cumsum = np.cumsum(fp)
# 计算precision和recall
precision = tp_cumsum / (tp_cumsum + fp_cumsum)
recall = tp_cumsum / len(gt_boxes)
# 计算AP(使用11点插值法)
ap = 0
for t in np.arange(0, 1.1, 0.1):
if np.sum(recall >= t) == 0:
p = 0
else:
p = np.max(precision[recall >= t])
ap += p / 11
return ap
mAP (mean Average Precision)
mAP 是多个类别上 AP 值的平均数，用于评估多类别目标检测模型的整体性能。
计算方法：
- 对每个类别计算 AP 值。
- 将所有类别的 AP 值进行平均，得到 mAP。
应用场景：
- 常用于目标检测比赛，如 COCO、PASCAL VOC 等，作为主要的评估指标。
特点：
- 考虑了所有类别的检测性能，提供了模型整体的性能评估。
- 适用于多类别且类别分布不平衡的情况。
计算mAP的代码示例（使用sklearn库）：
def calculate_map(pred_boxes_list, pred_scores_list, gt_boxes_list, num_classes, iou_threshold=0.5):
"""计算mAP
Args:
pred_boxes_list: 每个类别的预测框列表
pred_scores_list: 每个类别的预测分数列表
gt_boxes_list: 每个类别的真实框列表
num_classes: 类别数量
"""
aps = []
for cls in range(num_classes):
ap = calculate_ap(
pred_boxes_list[cls],
pred_scores_list[cls],
gt_boxes_list[cls],
iou_threshold
)
aps.append(ap)
mAP = np.mean(aps)
return mAP
Reference
- 机器学习基础---分类与检测的评价指标---AP，mAP，PRC曲线
- 分类问题中的一些指标概 念-Roc|AUC|Pre|Recall|ACC|AP|mAP|F1总结
- 分类器的ROC曲线及相关指标（ROC、AUC、ACC）详解
- MCC — 机器学习中优于F1-score和accuracy的一个性能评价指标
- Data Science in Medicine — Precision & Recall or Specificity & Sensitivity?