从自信息量到交叉熵&极大似然估计的数学推导
首先,我们需要认识什么是信息量与信息熵:
自信息量
通常自信息可以从两个方面来理解:
- 自信息是事件发生前,事件发生的不确定性。
- 自信息表示事件发生后,事件所包含的信息量。
(比如你看到这,会想问作者也许不是一只猫而是人类————那我当然不是猫,这就没有不确定性可言,没有什么信息量;如果有一天我真的是猫了,那便是大新闻了!!) 自然而然,我们会想到所谓信息量应当与概率有关,且应该可以加合(两个事件发生时带来的信息量应该是分别发生时的和),也就是满足以下特质:
- $f\left( P \right) >0 \; \; \; \; P\left( x \right) \in \left( 0,1 \right) $
- $f\left( P_A·P_B \right) =f\left( P_A \right) +f\left( P_B \right) $
- $f\left( 1 \right) =0$
- 事件发生概率越大,自信息量越小
此时我们可以才想到对数会满足这样的性质,于是可以给出:$I\left( x \right) =-\log \left( P\left( x \right) \right) $
因为在计算机领域中习惯用二进制,所以我们通常以2为底,这样自信息量的单位就为比特bit,——即二进制数的一位包含的信息或2个选项中特别指定1个的需要信息量。而机器学习中常选择以e为底,单位为奈特nats
你可以通过以下例题来更好的理解自信息量:

信息熵
接下来,我们将进一步研究什么是信息熵,在前面我们学会了如何衡量一个事件的不确定性,但一个随机变量可能包含的多个事件,我们该如何对这个 随机变量的不确定性 进行刻画呢? 我们会自然想到求出所有事件的信息量期望,且熵越大,事件的不确定性越强,当满足均匀分布时熵最大(有约束情况下要额外考虑,一阶矩二阶矩不同时的最大熵分布不同,详情可参考最大熵原理);如果熵值小,证明某个事件发生的概率比较大,随机变量取某个值的概率大,不确定性就小了。(另外,信息熵也可以理解为解除信源不确定性所需要的信息量) 于是我们给出: (其中规定)$0\log 0=0$ $$ H\left( x \right) =-\sum_{i=1}^n{p\left( x_i \right) \log \left( p\left( x_i \right) \right)} $$ 我们可以验证,当n个事件满足等概率分布时其中当结果为logn(n为总数)信息熵达到最大值。 另外可以给出条件熵(你可以运用条件概率辅助理解): $$ H\left( Y|X \right) =-\sum_x{\sum_y{p\left( xy \right) \log P\left( y|x \right) =\sum_x{-\sum_y{P\left( y|x \right) \log P\left( x \right) =\sum_x{P\left( x \right) H\left( Y|x \right)}}}}} $$
相对熵
如果我们对于同一个随机变量x有两个单独的概率分布P(x) 和 Q(x),我们可以使用KL散度(Kullback-Leibler (KL) divergence)或者叫相对熵来衡量这两个分布的差异情况,其中p对q的相对熵写作(在机器学习中,我们可以把P(x)看作真实分布,而Q(x)作为预测的分布):
$$
D_{KL}\left(p||q \right) =\sum_x{p\left( x \right) \log \frac{p\left( x \right)}{q\left( x \right)}=E_{p\left( x \right)}\log \frac{p\left( x \right)}{q\left( x \right)}}
$$
同时KL散度还满足以下条件:
$$
D_{KL}\left(p||q \right) \ne D_{KL}(q||p)
\
D_{KL}\left(
p||q\right) \geqslant 0
$$
对于第一个式子,我们可以借助以下内容理解:
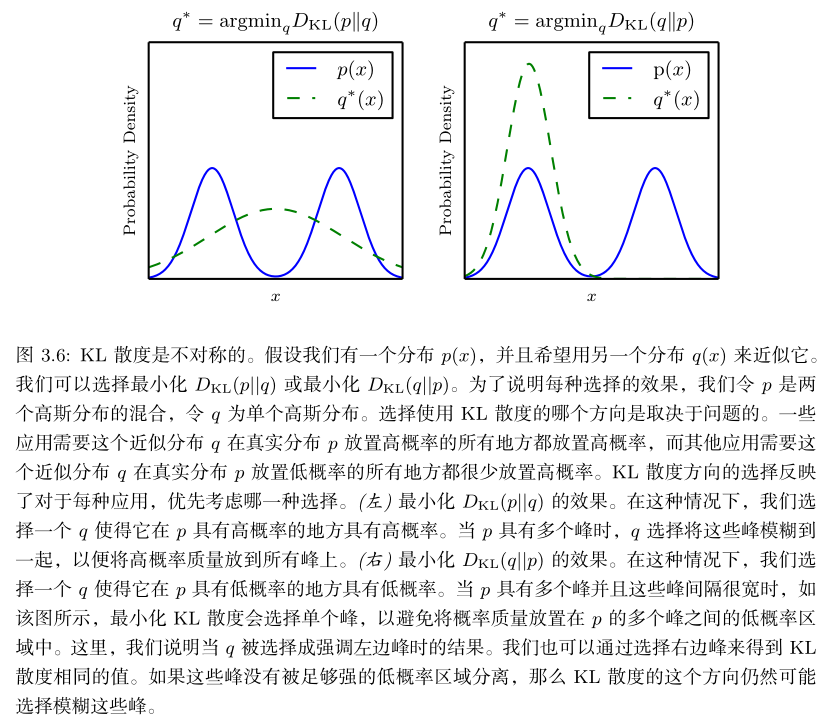 用比较通俗的话来说,让我们回到公式之中,且注意到P(x)作为真实分布,Q(x)作为预测的分布;
用比较通俗的话来说,让我们回到公式之中,且注意到P(x)作为真实分布,Q(x)作为预测的分布;
$$ D_{KL}\left( p||q \right) =E_{p\left( x \right)}\log \frac{p\left( x \right)}{q\left( x \right)} $$
- 当第一种情况,如果P(x)是较大的,那么q(x)也应该较大来保证相对熵最小化;如果P(x)是较小的,那实际上q(x)的大小对相对熵影响不大;所以我们只需要特别注意前者的情况。此时在看图你就可以更��加理解了。
$$ D_{KL}\left( q||p \right) =E_{q\left( x \right)}\log \frac{q\left( x \right)}{p\left( x \right)} $$
- 当第二种情况,很显然会与第一种情况相反,如果P(x)是较小的,那么q(x)也应该较小来保证相对熵最小化————这就是为什么说图中提到概率小的地方比较重要,而q(x)较大的时候就影响不大了。
交叉熵
接下来我们要了解常用的一种更常用的熵————交叉熵,由前面学到的相对熵可以进一步推导:
$$
\begin{aligned}
D_{KL}\left( p||q \right) &=\sum_{i=1}^n{p\left( x_{\mathrm{i}} \right) \log \left( \frac{p\left( x_i \right)}{q\left( x_i \right)} \right)}\
\mathrm{
}&=\sum_{i=1}^n{p\left( x_i \right) \log \left( p\left( x_i \right) \right)}-\sum_{i=1}^n{p\left( x_i \right)}\log \left( q\left( x_i \right) \right)\
&=-H\left( p \right) -\sum_{i=1}^n{p\left( x_i \right)}\log \left( q\left( x_i \right) \right)\
\end{aligned}
$$
其中第一项我们可通过推导得知是针对真实分布概率p(x)的信息熵,而后一项我们定义为交叉熵; $$ H\left( p,q \right) =-\sum_{i=1}^n{p\left( x_i \right)}\log \left( q\left( x_i \right) \right) $$ 交叉熵可以理解为,消除体系不确定性所需要付出的努力大小。
交叉熵与极大似然估计的联系
由于真实分布的信息熵是确定的,在优化过程中(最小化相对熵),我们可以把他忽略,只看交叉��熵的部分。此外,最小化交叉熵其实与极大似然估计是等价的,具体证明如下:(参考Deep Learning.Ian Goodfellow and Yoshua Bengio and Aaron Courville)
我们考虑一组含有m个样本的数据集$\mathbf{X}=({ x^{(1)},\cdots ,x^{(m)} }) $,此时可以定义 $ \theta $ 的极大似然为(其中P为模型的联合概率):(如果你不懂argmax是什么意思可以参考argmax科普)
$$
\begin{aligned}
\mathbf{\theta }_{ML}&=\underset{\theta}{\mathrm{argmax}}P_{model}\left( \mathbf{X};\theta \right)\
\mathrm{
}&=\underset{\theta}{\mathrm{argmax}}\prod_{i=1}^m{P_{model}\left( \boldsymbol{x}^{\left( i \right)};\theta \right)}
\end{aligned}
$$
由于乘积不好计算,我们可以取log将他转换为加和形式,取最值时的参数不变;且可以乘上不影响结果的 $ \frac{1}{m} $。
$$
\begin{aligned}
\mathbf{\theta }_{ML}&=\underset{\theta}{\mathrm{argmax}}\sum_{i=1}^m \mathrm{log} {P_{model}\left( \boldsymbol{x}^{\left( i \right)};\theta \right)}\
\mathrm{
}&=\underset{\theta}{\mathrm{argmax}}\frac{1}{m}\sum_{i=1}^m \mathrm{log} {P_{model}\left( \boldsymbol{x}^{\left( i \right)};\theta \right)}
\end{aligned}
$$
由大数定律可知(算术平均值依概率收敛于期望):
$$
\frac{1}{m}\sum_{i=1}^m{X_i\longrightarrow} \mu
$$
可以将原式进一步化为:
$$
\begin{aligned}
\mathbf{\theta }_{ML}&=\underset{\theta}{\mathrm{arg}\max}\mathbb{E}_{\mathbf{x}~\hat{p}_{data}}\log P_{model}\left( \boldsymbol{x};\boldsymbol{\theta } \right)\
&=\underset{\theta}{\mathrm{arg}\max}\sum_x{p\left( x \right) \log q\left( x \right)}\
&=\underset{\theta}{\mathrm{arg}\min}\left[ -\sum_x{p\left( x \right) \log q\left( x \right)} \right]\
\end{aligned}
$$
Bravo!!! 此时你惊喜的发现这就是我们前面推导得到的交叉熵公式,至此,对于真实分布和模型分布,我们明白了MLE方法(让似然最大化)等价于两者间交叉熵的最小化。好奇的你也许想问“MLE与KL散度也是共通的吗?”————这个问题你可以自己试试看,就用上式类似办法加常数即可!